楊雯雯
在臨床診斷治療上,醫療人員經常得面對各種疾病篩檢、診斷檢驗或檢查、治療成效的不確定性,因而需要透過系統性的搜尋實證文獻來協助確立診斷與決定治療。然而,透過所搜尋到論文,要從那些數據才能了解該診斷工具的效能呢?又如何應用該診斷工具檢驗的結果呢?
一、診斷工具的效能(performance)
通常我們可以利用診斷科技之文獻所提供的幾樣數據(例如,有多少有病的人被正確檢驗出來),再做簡單的計算就能知道該項檢驗或檢查的效能。首先,我們可以摘錄文獻中所提供的數據,建構一個 2X2 的列聯表,如表一。第 3 和第 4 欄位名稱,指的是文獻提供有關受測者原本有無疾病的分類(通常是經該疾病領域被公認的黃金標準(gold standard)所診斷確認的結果),第 3 和第 4 列名稱指的是新診斷工具的檢驗結果。這讓我們更清楚了解該新診斷工具在所有受測者中,能區分有無罹病的能力。當然理想中,一個完美的診斷工具應該不會有偽陽性和偽陰性,也就是說對我們所關心的疾病,能正確檢驗分辨出到底有無該項疾病,可惜並不是所有診斷工具或檢驗方法都如此完美。於是我們想知道該診斷工具的效能,如敏感度(sensitivity)、特異度(specificity)、精確度(accuracy)、陽性預測值(positive predictive value, PV+)和陰性預測值(negative predictive value, PV-)等,以了解陽性結果代表多大的機會真的是有病。後續段落將就表一的 4 個細格,分別描述所代表的意義:
表一、 檢驗結果與罹病狀況的2X2列聯表

真陽性(true positive, TP)表示在真正有病的族群中,檢驗的結果也真的是陽性。
真陰性(true negative, TN)表示在沒病的族群中,檢驗的結果也是陰性。
偽陽性(false positive, FP)表示在沒病的族群中,檢驗的結果卻是陽性。
偽陰性(false negative, FN)表示在真正有病的族群中,檢驗的結果卻是陰性。
在對某疾病做篩檢時,由於民眾通常不清楚自己有沒有病,此時若篩檢結果發生偽陰性(有病但檢驗結果是陰性),則對那些延遲治療恐致嚴重後果的疾病來說,將是一個可怕的結果。以2009年美國疾病管制暨預防中心(U.S. Centers for Disease Control and Prevention, CDC)檢測三種新型流感H1N1病毒感染的商用快速篩檢試劑為例[1],CDC發現相對於即時反轉錄多聚酵素連鎖反應(rRT-PCR)檢驗,這三種快速篩檢檢測的敏感度只在 40% 到 69% 之間,CDC進一步說明:試劑結果呈現陰性也不排除有感染新型流感H1N1病毒,就是說可能有 31% 到 60% 受測者的檢體即使有H1N1病毒,可能也沒被驗出來,這恐會忽略感染而導致症狀惡化。相對的,對偽陽性而言(沒有病但檢驗結果是陽性),則可能導致這些人接受不必要的治療,特別是當治療本身有高度危險性時,更應謹慎。例如,Omidiji 等人的研究以超音波相對於以組織的病理變化來做乳癌篩檢,結果得到 100% 的高敏感度和22%的低特異度結果[2],也就是說,只使用超音波作為乳癌篩檢將有較高的偽陽性,若這些偽陽性者都被送去做乳房切除,將會造成多大的傷害呀。因此,若真要選擇一種診斷或檢驗工具,我們便會希望獲得更多有關效能的資訊,以便幫助判斷是否要採用該檢驗工具。
敏感度(sensitivity)是指在所有罹病的群體中,經某診斷檢驗或檢查後,結果是呈陽性的百分比,又稱為真陽性率(true positive rate,TPR)。這種基於某種情況下,才發生某件事的機率,在數學上會利用條件機率來表示,例如,p[positive|Disease] 意指在有 Disease 的情況下,是 Positive 的機率。其計算公式如下:

特異度(specificity)是指在所有沒病的群體中,經某診斷檢驗或檢查後,結果是呈陰性的百分比,又稱為真陰性率(true negative rate,TNR),其計算公式如下:

敏感度和特異度可以作為診斷工具一致性(concordance)的指標,數值愈高愈好;相對的,偽陽性率和偽陰性率可作為不一致性(discordance)的指標,數值愈低愈好。所謂的偽陰性率(false negative rate, FNR)是指有病的人,經工具診斷,結果卻是陰性的比率,也等於用1減掉敏感度(1-sensitivity);偽陽性率(false positive rate, FPR)則是指,沒病的人卻被診斷為陽性的比率,亦等於1減掉特異度(1-specificity)。計算公式分別如下:

精確度(accuracy)也是診斷工具效能的另一種參考指標,精確度是指所有病人中真陽性加真陰性所占的比例,其計算公式如下:

在決定診斷工具時,陽性預測值(positive predictive value, PV+)和陰性預測值(negative predictive value, PV-)通常也是展現效能的一種參考指標。陽性預測值是指在陽性診斷結果下,病人真有病的機率;陰性預測值是指在陰性診斷結果下,病人真的沒病的機率。這就像我們處於某種情況下,想知道發生某種件事的機率,數學上同樣可以利用條件機率來呈現公式;但這裡我們必須留心,在評估診斷工具效能時,我們不能單單只看陽性預測值或陰性預測值,因為,縱使敏感度和特異度維持一樣,陽性預測值和陰性預測值其實都會受到疾病盛行率(prevalence)的影響:

這裡的盛行率在診斷工具試驗中是指所有受試者中真正有病的機率:

舉例而言,若要評估一種新的 HIV-1 病毒快速篩檢法-濾紙乾血法(Rapid method for screening dried blood samples on filter paper),做為未來疑似感染 HIV-1 病毒的抗體檢查,研究數據告訴我們新方法總共篩檢了 140 位受試者,其中 62 位受試者以傳統標準的 RT-PCR 檢驗已確認是 HIV-1 感染者,剩餘 78 位並沒有感染,新方法篩檢的結果如表二,則新方法的敏感度和特異度到底為何?
表二、濾紙乾血法檢驗結果與感染狀況的2X2列聯表(n=140)

透過前面 (1)、(2)、(5) 和 (8) 的公式計算,我們可以分別得到敏感度、特異度和精確度分別為 0.935、0.987 和 0.964。我們通常期望這三個數值愈大愈好,最好是百分之百,但事實上不容易遇到,於是我們要考慮所要篩檢的目的是什麼?若所欲篩檢的是致死性或高傳染性疾病,如癌症或立百病毒(Nipah virus)感染症等,則診斷工具應優先要求有較高的敏感度,希望盡可能找出真正罹病或感染的人。表二計算結果如下:

如同 HIV-1 病毒快速篩檢法-濾紙乾血法的例子,若進一步想知道當濾紙乾血法檢驗為陽性結果時,有多少程度病人真的是有 HIV-1 病毒感染,或是當濾紙乾血法檢驗為陰性結果時,真的能安心認為沒有感染嗎?於是我們利用公式 (6) 和 (7) 計算陽性預測值和陰性預測值的結果分別為 0.983 和 0.951。經由這些結果我們知道這快速篩檢診斷工具的效能還算不錯,但陰性預測值為 0.951,換句話說,若我們採用這種濾紙乾血法來篩檢民眾,則接受篩檢的民眾其結果是陰性時,還是有 0.049 的機會其實已經有 HIV-1 感染,若這些民眾以為自己是健康的,繼續從事 HIV-1 感染高危險性的活動,則傳播風險是可以被接受的嗎?因此,對於檢驗結果是陰性的人卻經常從事 HIV-1 感染高危險性活動者,將會建議定期追蹤或是進行後續檢驗。計算過程如下:

延伸此例,若我們知道這 HIV-1 病毒濾紙乾血法的敏感度為 0.935,特異度為 0.987,與之前研究的數值一樣,但這一次的試驗,總共篩檢 20,000 位受試者,其中 10,000 位受試者以傳統標準的 RT-PCR 檢驗,確認是 HIV-1 的感染者,剩餘 10,000 位沒有感染,詳細結果如表三,則陽性預測值和陰性預測值分別為何?
表三、濾紙乾血法檢驗結果與感染狀況的2X2列聯表(n=20,000)

一樣透過前面(1)到(8)的公式,我們可以分別再計算出敏感度、特異度、精確度、陽性預測值和陰性預測值,分別為 0.935、0.987、0.961、0.986 和 0.938,由此我們發現精確度由 0.964 變成 0.961,陽性預測值由 0.983 變成 0.986,陰性預測值由 0.951 變成 0.938。可見若要評估一個診斷工具的效能,單看一個指標表現是不足夠的,有時是十分危險的。計算過成如下:

如同陽性和陰性預測值,概似比(likelihood ratio, LR)也分為陽性概似比(LR+) 和陰性概似比(LR-)。陽性概似比意指真正罹病的人檢查結果為陽性之比例,「除以」真正沒病的人但檢查結果為陽性之比例;陰性概似比則指真正罹病的人但檢查結果為陰性之比例,「除以」真正沒病的人檢查結果也呈陰性之比例。從定義和公式中可知,這兩種概似比和敏感度與特異度有極大的關係,但是和盛行率無關。因此,概似比也經常被用來作為評估診斷工具效能的一種指標。計算公式如下:

在濾紙乾血法的例子中,無論盛行率是 0.443 或 0.5,陽性概似比和陰性概似比的值都為 71.923 和 0.066,並不會受到盛行率影響。計算過程如下:
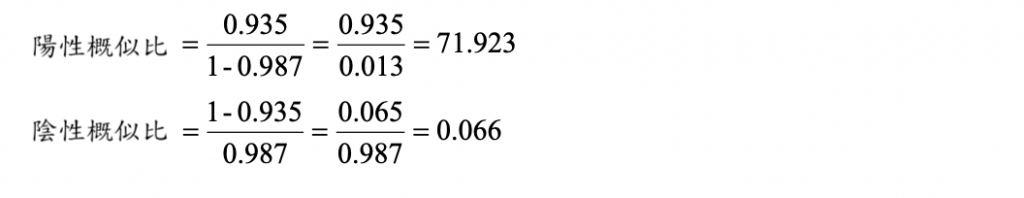
概似比的高低大小如何解釋呢? Ebell 在 2001 年參考 Sackett 等學者提出概似比在臨床意義的說明[3](請見表四),這提供我們對概似比解釋有一個尺度參考。在濾紙乾血法的例子,陽性概似比的值為 71.923,遠大於 10,當診斷結果是陽性時,有病是沒病機率的 71 倍,亦即高度認為求診者是有 HIV-1 感染的;反之,陰性概似比的值為 0.066,遠小於 0.1,當診斷結果是陰性時,有病是沒病機率的 0.066 倍,證據夠強到可排除求診者有 HIV-1 的感染(這是基於求診者沒有其他因素影響,但若求診者有從事或接觸感染高危險性事務時,則感染 HIV-1 之勝算將隨之改變)。
表四:概似比的臨床意義

除了像濾紙乾血法這種二元類型診斷結果的例子,概似比尚可應用於多層級(multiple levels)結果的診斷工具上。一篇文獻測試以修飾的加強型 p24 抗原來預測 HIV-1 RNA 的病毒量,作者指出以 Amplicor HIV-1 Monitor testing 作為標準檢驗,共評估 283 份血清樣本以修飾加強型 p24 抗原檢驗後的結果,作者所計算出各層級的概似比,如圖一[4];圖中最下一列,可見該試驗以標準方法檢測病毒量大於 5.5 log copies/ml 的人有 26 位,小於 5.5 log copies/ml 的人有257位;圖中結果的第一列指出 p24 抗原大於 4 log fg/ml 的陽性概似比為 7.91,也就是說當檢驗 p24 抗原結果大於 4 log fg/ml的時候,病毒量大於 5.5 log copies/ml的機會是小於 5.5 log copies/ml 的 7.9 倍;同樣的計算程序重複於各層級(結果列之第 2 至 5 列)。參考 (9) 和 (10) 公式,我們可以將其計算邏輯表示為:


2001 年 Ebell 針對臨床意義、是否受盛行率影響、是否能運用在具多層級(multiple levels)結果的診斷工具,提出敏感度/特異度、預測值和概似比的比較(請見表五)。Ebell 認為醫療人員面對求診者時,通常不清楚所面對的人是不是有病,因此,敏感度與特異度相對於預測值和概似比,在臨床使用上是不具意義的;除此,預測值會受到盛行率影響而顯得不穩定;三種效能指標中,只有概似比可以運用在多層級的診斷結果上,因此 Ebell 認為概似比的實際應用會日漸增多。
表五:診斷工具效能指標的比較

大家都會期望所使用的診斷工具可以完完全全將有病和沒病的人區分出來,但許多診斷工具在實驗測試階段就會產生數個結果。如圖二,在有病(diseased population)和沒病(healthy population)的人群分布中,診斷工具有時難免會出現偽陽性或是偽陰性的結果,如同前面段落所提,我們經常得依疾病特性或是治療風險性來判斷能容忍多少比例的偽陰性和偽陽性。如圖二,當切線(cutoff value)C點往右邊移時,雖然偽陽性(C至D)減少了,但是偽陰性(C至B)卻增加了,也就是增加了特異度(C至A),但減少了敏感度(C至E);反之,當cutoff value往左移動時,偽陰性減少而偽陽性增加了,亦即特異度減少而敏感度增加。診斷工具在開發過程,可能因試驗執行數次而產生數個結果,因此經常會利用幾次的敏感度和特異度數據來形成一個便於視覺觀察的曲線,如圖三。

圖三中藍色曲線(good test)和紅色曲線(worthless test),又稱作接受操作特徵曲線(receiver operating characteristic curve, ROC curve),雙軸分別由敏感度(即真陽性率)和1-特異度(即偽陽性率)所構成。在許多的測試點中,我們期望曲線愈偏左上角愈好(如藍線),也就表示診斷工具的效能愈佳,診斷結果的真陽性率愈高,偽陽性率愈小;相對於區線愈偏向對角線(如紅線),則表示效能愈差。有些時候,同時有數個類似的診斷工具需要我們選擇時,僅由每一診斷工具的接受操作特徵曲線還是令人難以比較,因此有另一種方式可以幫助我們衡量不同診斷工具間的效能,那就是比較接受操作特徵曲線下的面積(area under the ROC curve, AUROC),這面積的範圍由 0.5 到 1.0,分別代表效能由差到佳,目前這也是多數探討診斷工具效能的論文中,會在文章中提供的數據。由此數據我們就能比較相似診斷工具用於篩檢某一疾病的效能,藉以選擇操作特徵曲線下面積最大的診斷工具。

二、診斷結果的應用
在了解診斷工具的各項效能指標後,假設我們依醫院的財務能力選購了一個最適當且操作方便的診斷工具,下一步我們便是希望在面對求診個案時,該診斷工具的檢驗結果能代表多少罹病的機率(即 p[Disease | Result]),整體而言,我們可由三種方法來得到答案,分別為條件機率、概似比及列線圖。
第一種方法是利用條件機率的觀念,可以想像在診斷工具檢驗結果已知的狀況下,來看罹病的機率,亦即:

將檢驗結果(Result)分別以陽性或陰性替代,就可以分別得到檢驗報告是陽性或陰性結果的狀況下,真正罹病的機率(當診斷工具的結果是陽性或陰性時,真正罹病的機率是多少?):

和

假若檢驗結果以二元的方式來看,由前一節已知

和

,這裡的

相當於該診斷工具試驗中的疾病盛行率;因此,上面的公式也可轉換成下面的表示方法:

舉例而言,依據一篇文獻所提供的數據,告訴我們在1831個檢體中有164個檢體是有A型流感病毒感染的,若以某快速抗原篩檢試劑檢驗,發現敏感度和特異度分別為 23.8% 和 99.5%[5],於是我們想知道當求診患者的抗原快篩檢體是陽性反應時,到底有多少的機率是感染到A型流感病毒?以及當檢體呈陰性反應時,還是有多少的機率是感染A型流感病毒?我們可以直接以公式 (15) 和 (16) 計算抗原快篩結果陽性/陰性的罹病率,亦或用已知的數據畫出 2X2 列聯表(請見表六),然後再利用敏感度和特異度推算出未知的細格(即TP、FP、FN、TN),最後再以公式 (15) 和 (16) 計算出陽性/陰性快篩結果的罹病率,過程如下:
- 畫 2X2 列聯表並填入已知數據,如表六
- 利用敏感度公式 (1) 及已知數據推算真陽性(TP)和偽陰性(FN)數值
- 利用特異度公式 (2) 及已知數據推算真陰性(TN)和偽陽性(FP)數值
- 將 2 及 3 推算之 TP、FN、TN、FP 數值填入 2X2 列聯表,如表七
- 利用公式 (15) 計算抗原快篩結果陽性的罹病率,計算結果為 0.8298
- 利用公式 (16) 計算抗原快篩結果陰性的罹病率,計算結果為 0.0701
由 5 及 6 的計算結果,我們得知以抗原快速篩檢試劑檢驗是否有 A 型流感病毒感染時,若結果是陽性時,可以估計已經感染的機率是 82.98%,但若結果是陰性時,還是有 7.01% 的機率是有感染的。
表六、A 型流感病毒抗原快篩結果與感染狀況的 2X2 列聯表 1/2

表七、A 型流感病毒抗原快篩結果與感染狀況的 2X2 列聯表 2/2

眼尖的人可能發現公式 (15) 陽性診斷結果的罹病率,其實計算結果和前一節診斷工具陽性預測值的結果一樣;公式 (16) 則與陰性預測值一樣。由公式中,我們知道它們都受到盛行率的影響,換句話說,若單由某項診斷工具的測試結果就斷定前來求診個案的罹病率是有風險的,因為實驗中,經抽樣後受測者的疾病分布不能完全推論到現實環境中的疾病分布。例如,前面 A 型流感的樣本主要是收集自 2009 年 4 月到 5 月間美國的檢體[5],研究當時的盛行率和同年 9 月全球大流行時的盛行率已經不同,也和我國的盛行率不同。因此,在做臨床決策時,經常會使用第二種方法來估計真正罹病的機率,即利用概似比(likelihood ratio)來估計。估計的過程會運用到簡單的貝氏理論,簡而言之,醫療人員在決策時,透過實證方法取得額外的資訊(某診斷工具的概似比),並根據這額外的資訊來修正原本的訊息(例如某特定疾病的盛行率)。例如,假設依據其他國家的經驗來看,大約會有 30% 的人口感染 A 型 H1N1 流感病毒,也就是說得 H1N1 流感的勝算是

(可用公式(20)計算而得)。
假設現在有一個發燒、咳嗽的病人來求助醫師,醫師為了要確定診斷,於是安排病人接受陽性概似比為

(可用公式 (10) 計算而得)的A 型流感快速篩檢試劑檢驗。報告出爐了,快篩結果呈現陽性,醫師於是重新估算這病人感染A型流感病毒的勝算為

(以公式 (17) 計算而得),也就是有 95.33% 的機率(以公式 (19) 計算而得)這病人真的是罹患 A 型流感(參見圖四的計算過程)。亦即我們初步對特定疾病所了解的罹病勝算(prior odds),會受進一步資訊的影響,而更新為新的罹病勝算(posterior odds),以公式表示為:

這裡的 likelihood ratio(概似比)指的概念和公式 (9) 至 (11) 是一樣的,只和診斷工具的敏感度與特異度有關,本身不會受到試驗中疾病盛行率的影響。透過公式 (19) 和 (20) 可以將公式 (17) 轉換為公式 (18),也就是在該診斷工具診斷的結果下,有病相對於沒病的勝算比。

這裡的勝算比是指一個事件會發生的機率除以不會發生的機率。因為,事件發生與否,經常帶著不確定性,於是我們經常用可能、或許,甚至用更精確的字眼,如事件發生的機率(probability, p)或是有多少勝算(odds)會發生來形容。在數學上,機率和勝算也是可以互換的,兩者的關係如下:


由於事後機率的判斷需要經過計算,在臨床繁忙的工作下,似乎有點緩不濟急,因此有第三種方法可以利用。早在 1975 年時,學者 Fagan 發展出一種列線圖(nomogram),現在我們只要利用這種列線圖(參見圖五左),將已知的事前機率對照到已知的概似比,就可以得到事後機率[6];如圖五右側圖,繼續以前述 A 型流感為例,我們已知事前機率(盛行率)和抗原快篩為陽性結果的罹病概似比分別為 30% 和 47.6,於是我們從第 1 條線 pretest probability(事前機率)找到 30 的位置,對照到第 2 條線 likelihood ratio(概似比)約為 47.6 的位置,然後在這兩點間畫一條線(這裡為紅色線)並延伸到圖中的第 3 條線 post-test probability(事後機率),從交點得知第 3 條線上的刻度大約為 95 多一些,也就是當盛行率高達 30% 時,經 A 型流感抗原快篩試劑檢驗結果為陽性者,其罹患A型流感的機率為 95.33%(事後機率)。雖然列線圖的刻度並不是十分細緻,但這種方法十分簡易,讓我們省卻許多計算的時間;除此,目前已有些網站(參見附錄)提供我們輸入事前機率和概似比,即可自動轉換成事後機率的功能。

有些時候,分辨是否真正罹病只用一種診斷工具是不夠的,例如A型流感的例子,求診個案在做抗原快篩檢驗後,即使結果是陰性,其實有A型流感的勝算還是高達 0.3282(依據公式 (11) 和 (17),事後勝算=

,亦即雖然抗原快篩陰性,但實際有病的機率仍有 0.2471),依據 Ebell 對概似比介於 0.2 到 0.5 間的解釋,我們只能低度排除沒有感染(參見表四)。若擔心偽陰性造成不良後果,在醫療資源與成本可接受的情況下,醫師決定安排進一步的檢驗:使用檢驗 H1N1 病毒敏感度和特異度分別為 0.993 和 0.923 的 rRT-PCR 檢驗試劑;假設新的檢驗結果為陽性,則這個病人罹患 A 型 H1N1 流感的機率變成多少?實務上這是常見的情形,需依賴數種診斷工具協助判斷;假設每一個檢查/檢驗事件是獨立的狀況下,我們將機率乘法原則的概念運用在一系列獨立的診斷結果上,簡單的說,第一次檢查的事後機率將成為第二次檢查的事前機率,第二次檢查的事後機率將成為第三次檢查的事前機率,依此類推,因為機率和勝算是可以互換的(公式 (19) 和 (20)),故我們將一系列的概念表達成圖六:

回到之前 A 型 H1N1 流感的例子,這病人歷經了兩次的檢驗,第一次快速篩檢試劑是陰性結果和第二次 rRT-PCR 檢驗是陽性結果,首先我們由 rRT-PCR 檢驗的敏感度和特異度計算出 rRT-PCR 檢驗的陽性概似比為

(可依公式 (10) 計算),然後將快速篩檢試劑陰性結果的事後勝算 (0.3282) 作為 rRT-PCR 檢驗的事前勝算,並乘以 rRT-PCR 檢驗的陽性概似比 12.90,於是我們得到新的陽性 rRT-PCR 檢驗之感染勝算為0.3282×12.90=4.2338(公式 (17)),亦即遭 A 型 H1N1 感染的機率從第一次快速篩檢試劑陰性結果的 0.2471,再經 rRT-PCR 檢驗陽性後,提高到了0.8089(參見圖七)。基於獨立事件的機率概念,這連續診斷結果的事後機率計算十分簡單。只是實務上,每次檢驗/檢查事件可能非全然是獨立事件,因此估計出來的數據可能會有高估的情形。

三、社區篩檢示例
嚴重特殊傳染性肺炎(COVID-19)自 2019 年 12 月 1 日爆發以來,迄 2022 年 5 月 12 日已造成全球累計超過518百萬的確診案例,6 百多萬人死亡,全台確診案例累計超過 50 萬人,950 人以上死亡。COVID-19 無疑是人類歷史上大規模流行的疾病之一,我國社會上自 2020 年以來,對於是不是要進行大規模篩檢的議題是爭論不斷。
現在有兩款輸入之 COVID-19 抗原快篩檢測套組,先不論檢測時間是否在最佳時間,以及試驗採用之循環閾值(cycle threshold value, Ct)為何,我們從仿單閱讀到兩款產品相較於 PCR 檢驗結果的臨床試驗數據(請見表八),從這些數據可以分別計算出各項效能指標,請見表九。
表八、COVID-19 抗原快篩結果與感染狀況列聯表

從表九的效能數據中,我們可以說兩款的效能都達到一定水準(當然,他們都取得食品藥物管理署的輸入販售許可)。不過,我們還是可以從兩者的比較數據發現乙抗原快篩較優。以甲抗原快篩來說,偽陰性率 13.6%、陰性預測值 94.6% 及陰性概似比 0.137,都劣於乙抗原快篩,如果今天我們是採取清零政策,那使用甲抗原快篩就可能讓更多有感染的人回到社區,導致社區破口,甚至因此延誤治療而惡化。
表九、兩款 COVID-19 抗原快篩檢測套組之檢測效能

接著來考量是否要大規模篩檢,雖然不知道我國實際感染 COVID-19 病毒的盛行率,我們就先用中央流行疫情指揮中心分別在 2020 年 4 月 27 日及 2022 年 5 月 11 日公布通報案例數及確診數來充當盛行率來源:2020 年 4 月 27 日通報案例數為 60,955,確診數為 429,盛行率為 0.007;2022 年 5 月 11 日通報案例數為 9,191,841,確診數為 505,455,盛行率為 0.055。除此,亦依每十萬人感染盛行率自 10 人至50,000 人來呈現兩款抗原快篩試劑的篩檢結果(請見表十)。
陽性預測值是指當我們在社區進行篩檢時,抗原快篩試劑陽性結果的人有多少百分比是真正有病的人;反之,陰性預測值是指抗原快篩試劑陰性結果的人,有多少百分比是真正沒病的人。從表十可見當盛行率愈低時,陽性預測值愈低,陰性預測值愈高,愈可能高估盛行率。此外,篩檢工具的敏感度和特異度也會影響陽性預測值和陰性預測值,敏感度和特異度愈高,陽性預測值和陰性預測值也會愈高。因此當社區感染盛行率極低時,進行大規模篩檢可能會找到較高比例的偽陽性民眾,除了須付出相當程度的篩檢成本外,對於被誤匡列為陽性接受隔離的民眾,更需額外付出社會成本,也會對民眾造成心理負擔。當然,引進高敏感度及高特異度的篩檢診斷工具,才能更有效的區分有感染和無感染的民眾,若在成本負擔及使用方便性相當的情況下,乙抗原快篩無疑是首選;而若篩檢工具如甲,或是較甲效能更差的工具,即使業者提供更優惠便宜的購買費用,我們仍應考量僅為了節省購買費用,需付出一定程度的偽陰性及偽陽性所衍生的後果是否值得。
表十、社區不同COVID-19盛行率下使用兩款抗原快篩之結果

總之,無論是要評估診斷工具的效能或是要將診斷工具測試的結果應用到實務,當我們閱讀診斷性論文或是仿單時,不時都要回頭再想想自己閱讀的目的是什麼,是為了自多種工具中選擇一種適合所屬單位使用的工具,還是為了臨床個案診斷之用?不同的目的在擷取論文數據時,會有不同的重點。因此,釐清閱讀目的是首要。
參考文獻:
- Centers for Disease Control and Prevention (CDC). Evaluation of rapid influenza diagnostic tests for detection of novel influenza A (H1N1) Virus – United States, 2009. MMWR Morb Mortal Wkly Rep. 2009 Aug 7;58(30):826-9.
- Omidiji OA, Campbell PC, Irurhe NK, Atalabi OM, Toyobo OO. Breast cancer screening in a resource poor country: Ultrasound versus mammography. Ghana Med J. 2017 Mar;51(1):6-12.
- Ebell MH. Evidence-based diagnosis: a handbook of clinical prediction rules. Berlin, New York, Vienna: Springer, 2001.
- Vanprapar N, Sutthent R, Chokephaibulkit K, Phongsamart W, Chearskul P. Modified Boosted-p24 Antigen can Predict HIV-1 RNA Viral Load (Ampiclor HIV-1 Monitor). Siriraj Med J 2005:57:173-6.
- Ginocchio CC, Zhang F, Manji R, Arora S, Bornfreund M, Falk L, Lotlikar M, Kowerska M, Becker G, Korologos D, de Geronimo M, Crawford JM. Evaluation of multiple test methods for the detection of the novel 2009 influenza A (H1N1) during the New York City outbreak. J Clin Virol. 2009 Jul;45(3):191-5.
- Fagan TJ. Letter: Nomogram for Bayes theorem. N Engl J Med. 1975 Jul 31;293(5):257.
附錄:
Bayesian calculator
網址:http://psych.fullerton.edu/mbirnbaum/bayes/bayescalc.htm
Diagnostic Test Calculator
網址:http://araw.mede.uic.edu/cgi-bin/testcalc.pl
Post-test probability calculator
網址:https://sample-size.net/post-probability-calculator-test-new/
Likelihood Ratio Nomogram – JAMAevidence
網址:https://jamaevidence.mhmedical.com/data/calculators/LR_nomogram.html

